Tag: c++

There is an undirected tree with n nodes labeled from 0 to n - 1, rooted at node 0. You are given a 2D integer array edges of length n - 1 where edges[i] = [a<sub>i</sub>, b<sub>i</sub>] indicates that there is an edge between nodes a<sub>i</sub> and b<sub>i</sub> in the tree.

At every node i, there is a gate. You are also given an array of even integers amount, where amount[i] represents:

• the price needed to open the gate at node i, if amount[i] is negative, or,
• the cash reward obtained on opening the gate at node i, otherwise.

The game goes on as follows:

• Initially, Alice is at node 0 and Bob is at node bob.
• At every second, Alice and Bob each move to an adjacent node. Alice moves towards some leaf node, while Bob moves towards node 0.
• For every node along their path, Alice and Bob either spend money to open the gate at that node, or accept the reward. Note that:
  • If the gate is already open, no price will be required, nor will there be any cash reward.
  • If Alice and Bob reach the node simultaneously, they share the price/reward for opening the gate there. In other words, if the price to open the gate is c, then both Alice and Bob pay c / 2 each. Similarly, if the reward at the gate is c, both of them receive c / 2 each.
• If Alice reaches a leaf node, she stops moving. Similarly, if Bob reaches node 0, he stops moving. Note that these events are independent of each other.

Return the maximum net income Alice can have if she travels towards the optimal leaf node.

Example 1: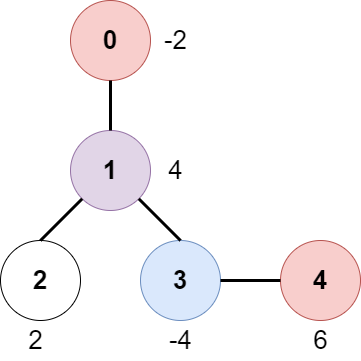

Input: edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6]
Output: 6
Explanation: 
The above diagram represents the given tree. The game goes as follows:
- Alice is initially on node 0, Bob on node 3. They open the gates of their respective nodes.
  Alice's net income is now -2.
- Both Alice and Bob move to node 1. 
  Since they reach here simultaneously, they open the gate together and share the reward.
  Alice's net income becomes -2 + (4 / 2) = 0.
- Alice moves on to node 3. Since Bob already opened its gate, Alice's income remains unchanged.
  Bob moves on to node 0, and stops moving.
- Alice moves on to node 4 and opens the gate there. Her net income becomes 0 + 6 = 6.
Now, neither Alice nor Bob can make any further moves, and the game ends.
It is not possible for Alice to get a higher net income.

Example 2:

Input: edges = [[0,1]], bob = 1, amount = [-7280,2350]
Output: -7280
Explanation: 
Alice follows the path 0->1 whereas Bob follows the path 1->0.
Thus, Alice opens the gate at node 0 only. Hence, her net income is -7280. 

Constraints:

• 2 <= n <= 10<sup>5</sup>
• edges.length == n - 1
• edges[i].length == 2
• 0 <= a<sub>i</sub>, b<sub>i</sub> < n
• a<sub>i</sub> != b<sub>i</sub>
• edges represents a valid tree.
• 1 <= bob < n
• amount.length == n
• amount[i] is an even integer in the range [-10<sup>4</sup>, 10<sup>4</sup>].

#include <vector>
#include <climits>
using namespace std;

class Solution {
public:
    int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
        int n = amount.size();
        
        // Build adjacency list
        vector<vector<int>> graph(n);
        for (auto& edge : edges) {
            graph[edge[0]].push_back(edge[1]);
            graph[edge[1]].push_back(edge[0]);
        }
        
        // Find Bob's path to root
        vector<int> bobPath;
        vector<bool> visited(n, false);
        findPath(graph, bob, 0, visited, bobPath);
        
        // Set Bob's visitation times
        vector<int> bobTime(n, -1);
        for (int i = 0; i < bobPath.size(); i++) {
            bobTime[bobPath[i]] = i;
        }
        
        // Reset visited and run DFS for Alice
        visited.assign(n, false);
        return dfs(graph, 0, 0, bobTime, amount, visited);
    }
    
private:
    // DFS to find path from start to target
    bool findPath(vector<vector<int>>& graph, int start, int target, 
                  vector<bool>& visited, vector<int>& path) {
        visited[start] = true;
        path.push_back(start);
        
        if (start == target) return true;
        
        for (int next : graph[start]) {
            if (!visited[next]) {
                if (findPath(graph, next, target, visited, path)) {
                    return true;
                }
            }
        }
        
        path.pop_back();
        return false;
    }
    
    // DFS to compute Alice's maximum income
    int dfs(vector<vector<int>>& graph, int node, int time, 
            vector<int>& bobTime, vector<int>& amount, vector<bool>& visited) {
        visited[node] = true;
        
        // Calculate income at current node
        int income;
        if (bobTime[node] == -1 || bobTime[node] > time) {
            income = amount[node];  // Bob arrives after or never
        } else if (bobTime[node] == time) {
            income = amount[node] / 2;  // Simultaneous arrival
        } else {
            income = 0;  // Bob arrives before
        }
        
        // Check if leaf node
        bool isLeaf = true;
        for (int next : graph[node]) {
            if (!visited[next]) {
                isLeaf = false;
                break;
            }
        }
        
        if (isLeaf) {
            return income;
        }
        
        // Explore children and find maximum path income
        int maxChildIncome = INT_MIN;
        for (int next : graph[node]) {
            if (!visited[next]) {
                int childIncome = dfs(graph, next, time + 1, bobTime, amount, visited);
                maxChildIncome = max(maxChildIncome, childIncome);
            }
        }
        
        // If no children were explored (shouldn't happen in a valid tree from root),
        // but handle it safely
        if (maxChildIncome == INT_MIN) {
            return income;  // Should not occur as root has children
        }
        
        return income + maxChildIncome;
    }
};